ABSTRACT
This work studies the propagation of thermo-mechanical disturbances in bodies made of viscoelastic materials that might already be loaded such that they are undergoing large inhomogeneous time varying deformations.
In the process of this study we develop the general equations governing the thermo-mechanical motion of such disturbances and ones for internally constrained systems, provide the general structure of the solution, match the solution to existing results for the special case of time harmonic plane waves in elastic bodies and in viscoelastic bodies under constant homogenous loading, and consider some specialapplications.
The results of this work should have applications in the study of anisotropic and inhomogeneous bodies that are inhomogenously loaded with the possibility that these loads are time varying, and may become part of tools used for non-invasive and non-destructive testing of such bodies.
Many common materials are anisotropic and inhomogeneous. These include most polymers, composites, soft and hard tissues, and all kinds of bio-mass. Many bodies are undergoing static or time varying inhomogeneous loading. Examples can vary from conditions that result in or from earthquakes and landslides to composites and live tissues functioning in loaded structures and bio-MEMS.
Some of the contributions of this dissertation are to introduce a full, thermodynamically consistent, nonlinear viscoelastic model to represent the material, to properly introduce thermo-mechanical coupling, to remove current limitations on the pre-deformation to be static, homogenous and around the equilibrium, to remove existing restrictions on the rate of loading of the perturbations, and to consider perturbations in the presence of material constraints.
KINEMATICS AND BALANCE LAWS FOR THERMO-MECHANICAL PERTURBATIONS
Kinematics:
We consider a continuous material body with κo denoting the reference configuration and κ(t) denoting the current configuration at time t. We let X denote the position vector of particles in the reference configuration and x denote the position in the current configuration.
Balance Laws:
The prediction of material response requires the combination of several elements. In general, these elements include mathematical models describing the material’s response characteristics (constitutive equations), specific conditions describing the initial state of the matter(initial conditions), conditions describing how the specific body is being influenced by its surrounding (boundary conditions), and laws describing how to combine these elements (balance laws).The focus of this section will be on the balance laws. These laws have a special place in the theory of material response since they are the same for all materials, in contrast to constitutive equations that are different for each material.
Balance Equations for Small Thermo-mechanical Perturbations Superimposed on a Deforming Body:
We plan to study the response of a thermo-mechanically deforming body to superimposed infinitesimal thermomechanical perturbations. These perturbations may represent waves,for which we seek equations to describe. To construct these equations, we consider two thermo-mechanical loading histories: a base history and a total history.
The total history is constructed from the base history by adding an infinitesimal thermomechanical perturbation. The response of the material to both the base history and the total history can be obtained from the constitutive equations, and both histories must satisfy the balance laws.
THERMOELASTIC SOLIDS AND WAVE PROPAGATION IN THERMOELASTIC MATERIALS
Thermoelastic Solids:
A characteristic of the elastic response is that the unloading response is very close to the loading response, sufficiently so that the difference can be ignored. We will consider the response of a thermodynamic body to be the values of its specific free energy ψ, specific entropy η, Cauchy stress T, and heat flux vector q. We will denote the response by R and consider it to be a function of the current conditions of the material point, given in terms of the position in the reference configuration X, and current time t.
Thermo-elastic Constitutive Models for the Perturbations:
In the previous section we developed the balance laws and their boundary and jump conditions for the perturbations. We will now evaluate the constitutive equations for these perturbations.
We first start by decomposing the perturbation into elastic and thermal parts and then derive the perturbation term for the stress, followed by those for the free energy, entropy and heat flux. Finally, we evaluate the evolution rule for the perturbations of the internal parameter associated with thermal expansion and then integrate it to obtain a general solution.
THERMO-VISCOELASTIC SOLIDS AND WAVE PROPAGATION IN THESE MATERIALS
Viscoelastic materials are those which show stress relaxation at all magnitudes of loading, even at very small loads. Models normally describing viscoelasticity show rate-dependent response and even yielding-like behavior without the use of a yield function. As such, they normally are characterized as a different class of material response. Mechanical analogs to describe the phenomenon seen in viscoelasticity are constructed from springs and viscous dampers. For a nonlinear response, the components of these analogs can be nonlinear.
Viscoelastic Solids:
The results in this section are developed for a thermodynamically based nonlinear viscoelastic material model. As will be seen, the model is of single integral form, and can be shown to specialize at the limit of infinitesimal deformations to a general single integral linear thermodynamic viscoelastic response.
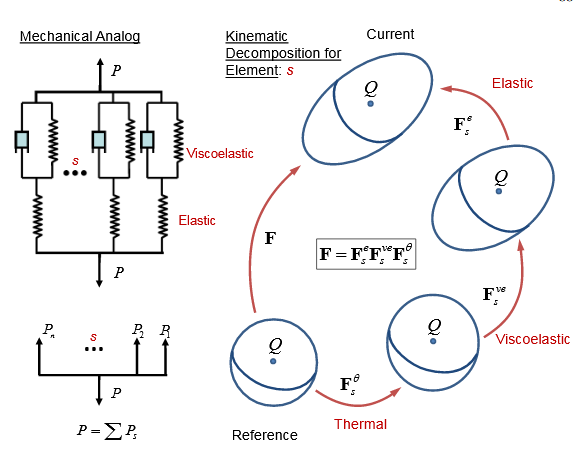
An Infinite Element Analog Constructed From Elements in Parallel That Each Separates Into a Thermal, Viscoelastic, and Elastic Element in Series.
PERTURBATIONS WITH MATERIAL CONSTRAINTS
Material constraints change the results for a thermodynamically consistent constitutive model. Material constraints refer to internal restrictions in the material such as incompressibility, where the volume of the material cannot change, or inextensibility, where material lines along a particular direction cannot change their length. In general, material constraints are idealizations, reflecting the difficulty of initiating one mode of deformation, for example, relative to other modes.
Material Constraints in Elastic Materials:
Let us look at the material constraints in the form of relations between components of the loadingL= (F,θ,G). For example, the constraint equation describing incompressibility is det(F) = constant,
since J = det(F) is the volume ratio relative to the volume in the reference configuration. Obviously the constant is unity if the reference configuration is taken to be a configuration that the material actually takes, such as the initial configuration.
The Effect of Material Constraints on Perturbations:
In this section, we will look at how the material constraints influence the perturbation equations. We will investigate the effect on the perturbations from the general material constraint which is studied in the previous section and mathematically can be expressed asC(F,θ,G,Fve,Fθ) = 0.
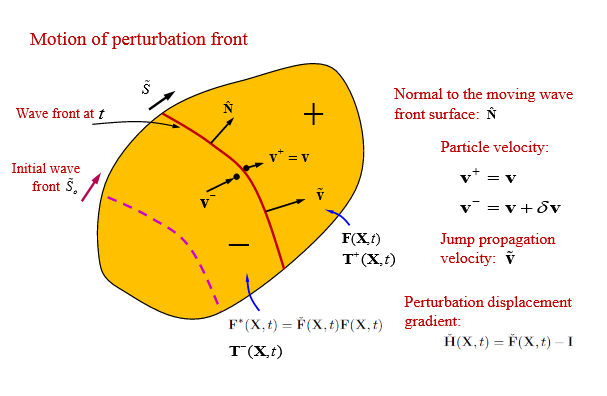
THE PROPAGATION OF MECHANICAL WAVES AND JUMPS IN INHOMOGENOUSLY DEFORMING VISCOELASTIC BODIES
The Propagation of Wave Fronts (Jumps) in Deforming Visoelastic Bodies:
Up to this point, we have assumed that all the base loadings and the perturbations are continuous and sufficiently smooth over all the body. Now we will look at the case when the perturbations are not sufficiently continuous, that is, in a volume the perturbation can be discontinuous over an entire surface, say S, yet continuous at all other points of the volume.
In this section we study the propagation of mechanical wave fronts (jumps) in inhomogeneously and homogeneously deforming and relaxing viscoelastic bodies. We select to look at the case where there is no discontinuity in the response of the base history, but there is a discontinuity in the perturbation.
CONCLUSION
This dissertation is primarily focused on studying the propagation properties of thermo-mechanical perturbations in deforming nonlinear materials, which include thermo-elastic solids and thermo-viscoelastic solids. The results are based on general nonlinear thermoelastic and thermo-viscoelastic constitutive modeling structures embedded into a thermo dynamically consistent framework, which permit large deformations and also large deformation rates under a broad range of temperatures.
FUTURE WORK
- Specifying the material model
- Studying the stability of the base history
- Studying the uniqueness and stability of the solution to the initial and boundary problem
- Special propagation properties of the perturbation
- Characterizing material properties
- Studying thermo-mechanical coupled waves
Source: University of Nebraska-Lincoln
Author: Lili Zhang